Osmotic Pressure, Surface Tension and Viscosity: Important Physical Forces Operating in Human BodyCHAPTER 1
Abbé Noller in 1748, placed pure water and solutions of alcohol in water on opposite sides of animals membranes that were more permeable to the solvent than to the solute molecules. He observed that the solvent (water) passed through the membrane from the water to the alcohol solution. This process is spoken of as osmosis (from the Greek word meaning push). Vierordt and Dutrochet found that hydrostatic pressure was caused by the process of osmosis. They called it osmotic pressure. Pfeffer in 1877, made the first attempt to measure osmotic pressure. Later van't Hoff deduced the laws of osmotic pressure from Pfeffer's data. All internal body fluids, extracellular and intracellular, possess one property in common, that is, an equal osmotic pressure. Kidney by regulating the volume and osmolality of urine maintains the osmotic pressure of extracellular and intracellular fluids. Various disturbances of extracellular and intracellular fluids during diarrhoea, plasma protein deficiency, burns and haemorrhage are treated employing principles of osmosis.
The interior molecules of homogeneous liquid are equally attracted in all directions by surrounding molecules. They are free to move in all directions. Therefore, free forces of attraction are not exhibited. But the situation is different in the liquid surface. The molecules of liquid in the surface are attracted downward and sideways but not upward (except for the little attraction of air molecules). Hence, the molecules of the surface are not so free to move as the interior molecules are. They are held together and form a membrane over the surface of the liquid. The force with which the surface molecules are held is called the ‘surface tension’. Laplace discovered that the property of surface tension generates 2a pressure in a bubble and makes it unstable. In lung, we have 300 million bubbles or alveoii. Nevertheless, such a mass of bubbles is not unstable like soap foam. In 1955, Pattle explained this phenomenon and said that it is due to the presence of pulmonary surfactant, a phospholipid secreted by type 2 alveolar cells. This surfactant lowers the surface tension of the liquid lining layer. Later Clements, in 1956, postulated that surface tension depends on the film area. Premature babies are deficient in lung surfactant and this leads to newborn respiratory distress syndrome. Factors reducing production of surfactant or increasing its rate of destruction may contribute to adult respiratory distress syndrome.
The best description of what we mean by ‘viscosity’ is still that given by Sir isaac Newton, who said it is a lack of slipperiness between adjacent layers of fluid. A fluid which obeys Newton's equation is said to be Newtonian. Water and simple fluids are Newtonian. Plasma is Newtonian but addition of red cells, however, makes the viscosity of blood anomalous. Viscosity of synovial fluid provides an index of severity of arthritis. Viscosity provides means for characterisation of the polymers (nucleic acids and proteins) from the point of view of its size, shape and conformation. In this chapter, physical forces like osmotic pressure, surface tension and viscosity have been discussed with special emphasis on their relevance in the functioning of human body.
OSMOTIC PRESSURE
Osmosis
Movement of molecules from a region of high concentration to a region of lower concentration due to random thermal molecular motion is diffusion. An ideal semipermeable membrane prevents diffusion of solutes but not solvent. In other words, a semipermeable membrane is permeable to water but impermeable to solutes. Osmosis is defined as the flow of water across a semipermeable membrane from a compartment in which the solute concentration is lower to one in which the solute concentration is greater. Osmosis takes place because the presence of solute decreases the chemical potential of water. Water tends to flow from where its chemical potential is higher to where its chemical potential is lower. Other effects caused by the decrease of the chemical potential of water (due to the presence of solute) include reduced vapour pressure, lower freezing point, and higher boiling point of the solution as compared with pure water. Because these properties as well as 3osmotic pressure depends on the concentration of the solute present rather than on its chemical properties, they are called colligative properties.
Osmotic Pressure
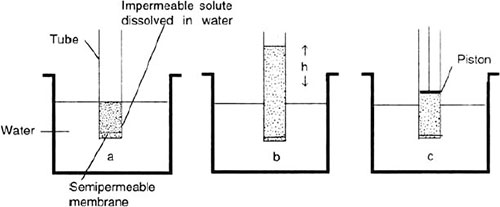
Osmosis can be stopped by applying hydrostatic pressure to the more concentrated solution to raise its water activity. The hydrostatic pressure which just stops osmosis is the osmotic pressure (Fig. 1.1). In other words, it is the pressure required to equalise water activities in the two compartments, osmotic pressure can be defined in terms of vapour pressure also. Osmotic pressure is the excess of pressure which must be applied to the solution in order to increase the vapour pressure until it becomes equal to that of the solvent.
Fig. 1.1: Phenomenon of osmosis and osmotic pressure. (a) Water flows through semipermeable membrane from outside into the tube. Tube contains solution of solute in water. This solute cannot pass through the semipermeable membrane. (b) Movement of water into tube's solution tends to dilute the solute. At equilibrium, the height of the column ‘h’ just counterbalances the osmotic pressure. (c) Osmotic pressure or the force that must be applied to exactly oppose the osmotic flow. Here, it is applied through piston in the tube. It is equal to the hydrostatic head ‘h’
van't Hoff pointed out striking resemblance between the osmotic pressure of solutions and the properties of gases. For example, the osmotic pressure of a given solution varies directly as the absolute temperature. This is similar to Charle's law for gas pressure, van't Hoff formulated the laws of osmotic pressure. These are stated below.
- The osmotic pressure of a solution varies directly with the absolute temperature in just the same way as the pressure of a gas varies when its volume is kept constant. Hence, the osmotic pressure can be expressed as:

where n/V is the number of moles of solute in volume V, R is universal gas constant and T is absolute temperature. This equation can be written as:

Where C is the molal concentration of the solution. This equation can be used for molecular weight determinations from osmotic pressure measurements. Suppose 2 g of a substance dissolved in 50 g of water (40 g in 1000 g of water) gives an osmotic pressure of 2.54 atm at 37oC, then the molal concentration C would be:

Thus, 40 g of the substance represents 0.1 mol, and the molecular weight of the substance accordingly is 400.
The osmotic pressure of a solution depends on the number of particles in solution, van't Hoff's law for calculating the osmotic pressure of ionic solution can be expressed as:
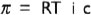
where π is osmotic pressure, R is ideal gas constant, T is absolute temperature, ‘i’ is number of ions formed by dissociation of solute molecule, and ‘c’ is molar concentration of solute (moles of solute per litre of solution). This equation applies more exactly to the very dilute solutions and does not predict precisely the osmotic pressure of real solutions. One way of correction, for the deviations of real solutions from the prediction of van't Hoff's law, is to use a correction factor called the osmotic coefficient (Ф). By including the osmotic coefficient the above equation becomes:

The osmotic coefficient may be greater or less than one. It is less than one for electrolytes of physiologic importance. The term Ф i c is often referred to as the osmolar concentration, with units in osmoles per litre. Solutions of proteins deviate greatly from van't Hoff's law, and different proteins may deviate to different extents.
Osmotic pressure can be estimated from another colligative property, such as depression of the freezing point. The equation describing this relation is as follows:
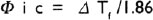
where ΔTf is the freezing point depression in degrees centigrade.
Determination of Osmotic Pressure of Biological Fluids
In dealing with biological fluids such as urine and serum the osmotic pressure is generally arrived at indirectly through the total molal concentration determined from freezing point measurements. The osmotic activity of physiological fluids is due to the combined osmotic activity of a number of substances which are dissolved in them. The lowering of the freezing point of a solvent by a solute is directly proportional to the ratio of solute to solvent molecules present. This relationship is expressed as:
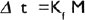
where ‘Δ t’ is the depression of the freezing point, Kf is the molal freezing point or cryoscopic constant, and M is the molal concentration of the solute. Osmotic pressures of solutions may also be obtained from measurements of boiling point elevation or vapour pressure lowering. However, neither of these methods is applicable to biological fluids.
Modification of van't Hoff's Equation
Biological membranes are not ideal but in varying degrees leaky. The osmotic pressure difference across such membrane (Δπ) is less than ideal and diminishes with time as some solutes diffuse through and eliminate their differences in concentration. The effective osmotic pressure will, therefore, be less and will depend on the degree to which solutes cross the membrane. This is expressed by including the reflexion coefficient ‘ σ ‘ in the van't Hoff's equation:

This equation can be modified if there are number of osmotically active solutes on two different sides of membrane:

6where Σ (C1-C2 is the sum of the difference in molar concentration of all osmotically active solutes on two sides of an ideal membrane. This equation can be modified for biological membrane as:

where σ is the reflexion coefficient. If none of the solute molecules colliding with the membrane cross it, σ = 1, that is, all molecules are reflected. If all the solute molecules pass through the membrane σ = 0, none is reflected and there is no osmotic pressure. The effective osmotic pressure of intracellular fluid often called its colloid osmotic pressure, is due to the large, reflected, non-penetrating solutes, e.g. proteins, organic phosphates. Some of these large solutes are negatively charged. Hence, attract small diffusible cations and repel small diffusible anions across the plasma membrane.
Net flow of water across the membranes: It is given by equation:
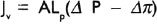
where Jv is the net flow of water across a membrane per unit time, A is the area of the membrane available for flow, Lp is hydraulic conductivity which is a measure of the ease with which water flows through membrane, (Δ P—Δ π) is the driving force. It is dependent on the differences in hydrostatic pressure (Δ P) and effective osmotic pressure (Δ π) across the membrane.
Units of Osmotic Pressure
To describe the effects of the total number of osmotically active particles per litre of solution the term osmolarity is used. It is wrong to speak of the osmotic pressure of a solution. An electrolyte like NaCl is dissociated in solution into two osmotically active ions, hence, its osmolar concentration will be approximately double of its molar concentration.
Maintenance, Regulation and importance of Osmosis and Osmotic Pressure
Osmotic Behaviour of Plasma Proteins
Some 90% by weight of plasma is water, about 8% is plasma proteins-albumin, globulins and fibrinogens. Albumin is the major contributor to the colloid osmotic (oncotic) pressure of the plasma because it has the lowest molecular weight of the major plasma proteins 7and its concentration is almost double than that of globulin. In addition, albumin binds with Cl− ions. This causes attraction and retention of cations in the vascular compartments and repulsion of diffusible anions. This leads to an uneven distribution of small ions and is referred to as the Gibbs-Donnan membrane distribution. As a result small excess of diffusible ions exist in plasma. This contributes about 9 mmHg to the effective osmotic pressure of plasma. Plasma proteins which cannot cross the capillary wall generate total plasma colloid osmotic pressure of 25 mmHg. However, this pressure is very small compared with the total osmotic pressure of all the solutes in plasma (5800 mmHg) measured when plasma is separated from pure water by an ideal semipermeable membrane.
Role of Plasma Oncotic Pressure in Tissue Fluid Formation
Filtration takes place at the arterial end of capillary because hydrostatic pressure of blood overcomes the oncotic pressure of plasma proteins. Reabsorption takes place at the venous end of capillary because hydrostatic pressure of blood falls below the oncotic pressure of plasma proteins. Net result of this filtration and reabsorption process is tissue fluid formation. The balancing of filtration/ultra-filtration and reabsorption/osmosis at arterial and venous end of capillary is referred to as the Starling equilibrium (Fig. 1.2). This equilibrium is not complete as there is slightly more ultrafiltration than osmosis. Starling equilibrium can be expressed by equation as:
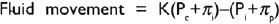
where Pc is capillary hydrostatic pressure, Pi is interstitial fluid hydrostatic pressure, πρ is plasma oncotic pressure, πi is interstitial fluid oncotic pressure and K is ultrafiltration constant for the capillary membrane.
If the ultrafiltration is excessive, the volume of interstitial fluid increases. When it becomes clinically detectable, it is called oedema. Venous obstruction, erect posture and plasma protein deficiency lead to oedema of this kind. Fluid reabsorption into capillaries increases after haemorrhage. Such response helps to restore blood volume. Excessive reabsorption also occurs during decreased venous pressure, arteriolar vasoconstriction and dehydration.8
Fig. 1.2: Effect of Starling forces leading to filtration at arterial end and reabsorption at venous end of capillary. ISF: interstitial fluid
Maintenance of Cell Volume
The determinants of cell volume are the total number of osmotically active particles within the cell and the osmolarity of the extracellular fluid. The cell has a considerable quantity of impermeant solutes, i.e. proteins and organic phosphates whereas the interstitial fluid is relatively devoid of these. Hence, their exist a colloid osmotic gradient across the cell and this would draw fluid into the cells. But this colloid osmotic effect of cell macromolecules is offset by the Na+-K+ pump which is capable of holding Na+ ions extracellularly. About 90% of the osmotic pressure of extracellular fluid is directly or indirectly due to sodium ions. Tonicity describes the behaviour of cells placed in a solution. If cells swell, the solution is hypotonic; if cells shrink, the solution is hypertonic; if cell volume is unchanged, the solution is isosmotic.
Maintenance of Body Fluids Osmolality by Kidney
Kidney maintains the optimum osmolality of body fluid by regulating the volume of the body fluids. Hence, when water intake is low or when water is lost through diarrhoea or perspiration, the kidney conserves water by producing a small volume of urine which is hyperosmotic. When water intake is high, the kidney excretes a large volume of hyposmotic urine. Normal osmolality of urine in 9males ranges from 390 to 1090 mOsm/kg and in females from 300 to 1090 mOsm/kg. Kidney maintains normal osmolality by regulating excretion of water and sodium chloride within a narrow range.
Variations of Osmosis
Dialysis, electrodialysis and ultrafiltration are the modifications of osmosis. Dialysis involves removal of smaller, crystalloidal particles from proteins or other colloids by selective diffusion through a membrane of appropriate permeability. Crystalloids and macromolecules are separated through dialysis (Fig. 1.3). Dialysis is used for separating salts employed in precipitation of proteins. For this, protein and salts in water are placed in cellophane sack. This sack is suspended in a large volume of water. Water outside cellophane sack is changed until no more salt ions are detected. In this way salts are washed out and desalting of proteins or other colloids is achieved. This desalting can be accelerated by electrodialysis, in which the protein is placed in the central chamber of a series of three, the compartments being separated by cellophane membranes. Electrodes are placed in the two outer chambers, and a current of electricity is passed through the system, causing rapid migration of diffusible ions (salts only) out of the central chamber.
Fig. 1.3: Explains the dialysis. The membrane of bag enclosing the protein solution allows the passage of water and small solutes, e.g. glucose or NaCl. But it does not permit passage of large solutes, e.g. proteins. By changing the outer phase with distilled water several times the concentration of small solute molecules in protein solution in bag can be decreased to almost zero level
10Artificial kidney is also based on the principle of dialysis. In artificial kidney blood flows continually between two thin sheats of cellophane; on the outside of the sheets is the dialysing fluid. The cellophane is porous enough to allow all constituents of the plasma except the plasma proteins to diffuse freely in both directions, i.e., from plasma into the dialysing fluid and from the dialysing fluid back into the plasma. If the concentration of a substance is greater in the plasma than in the dialysing fluid, there will be net transfer of the substance from the plasma into the dialysing fluid. Hence, the waste products and other substances in excess diffuse across the cellophane tubing and are eliminated from the body. Ultrafiltration is dialysis under pressure, the water and crystalloids being forced through the semipermeable membranes by the application of positive pressure from above the solution.
SURFACE TENSION
Definition
The force with which the surface molecules are held is called the ‘surface tension’ of the liquid. It is the force acting perpendicularly inwards on the surface layer of a liquid to pull its surface molecules towards the interior of the fluid. It keeps the surface like a stretched membrane, and hence keeps the contact area minimum. By minimising the area of the liquid surface, surface tension maintains the free surface energy at the minimum. It is expressed in dynes acting perpendicular to any imaginary line of 1 cm length of the liquid surface. The surface tension of water, mercury and either is 72.8, 465, and 21.7 dynes/cm, respectively. Surface energy is the potential energy per unit area of the surface film. Another term closely associated with surface tension is capillarity. The elevation or depression of liquids in capillary tubes is called capillarity. The height to which a liquid rises in a capillary depends on the surface tension, density of the liquid and radius of capillary.
Factors Affecting Surface Tension
Temperature
Surface tension falls with the rise in temperature.
Solutes
Solutes concentrating on the liquid surface lowers the surface tesion. On the other hand solutes dispersed in liquid raise surface tension.
Surface tension of a colloidal solution is not constant but decreases rapidly as a function of time. This is especially noticiable with albumin, alkaline soaps and bile salts.
Density
Surface tension has been related with density through Macleod's equation:

where p is the density of liquid and p’ is the density of its vapour.
Determination of Surface Tension
Capillary Method
The surface tension of a liquid can be determined from the height to which the liquid rises in a capillary that the liquid wets; it is given by the equation:

where ‘h’ is height to which liquid rises in the capillary, ‘d’ density of the liquid, ‘g’ acceleration due to gravity and ‘r’ capillary radius.
Hanging Plate Method
In this procedure, the lower edge of a thin wettable plate is dipped into a dish of water (Fig. 1.4). The wettable plate is suspended from a force-measuring device or transducer. The water ‘creeps up’ the sides of the plate and pulls downward with a certain force. This force is given by the equation:
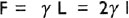
where F is the force in dynes, L is the total length of the water plate boundary in cm, I is the length of the plate and γ is the force per unit length (dynes per cm) along the boundary. The proportionality constant γ is called the surface tension at the water-air interface and measures about 72 dynes per cm. A plasma-air interface has a ‘γ’ of 40 to 50 dynes per cm.
Traubes Stalagmometer Method
This method is based on the fact that due to surface tension, a liquid will tend to form drops in an attempt to reduce the surface area to the minimum.12
Fig. 1.4: Hanging plate method of measuring surface tension. A thin clean platinum plate suspended from a force transducer is dipped into the liquid. The surface tension is directly proportional to the recorded force. This method permits continuous measurement of surface tension
If a liquid flows through a small opening, it will tend to form drops which will fall off when gravity force exceeds the surface tension. The number of drops formed from a given weight of volume of the liquid will depend upon its surface tension which can be calculated from the number of drops of liquid compared to the number of drops of the same weight or volume of water. To calculate surface tensions first the apparatus is filled with water upto the upper mark above bulb. Now, allow the water to run down till the level comes to the upper mark. Water is further allowed to fall but now the number of drops (Nw) falling are counted till the level reaches the lower mark. Similarly, the number of drops (N) formed for the given solution for which the surfaces tension is to be determined, are counted.
Surface tension of unknown solution = 8 w Nw S/N dynes/cm
where 8 w is the surface tension of water which is 73 dynes/cm, Nw is number of drops of water, N is number of drops of unknown solution and S is the specific gravity of unknown solution.
The Gibbs-Thomson Principle
According to this principle substances which lower the surface tension become concentrated in the surface layer whereas substances which increase surface tension are distributed in the interior of the liquid. Lipids and proteins effective in lowering surface tension, are found concentrated in the cell wall. Soaps and bile salts reduce the surface tension of water while sodium chloride and most inorganic salts increase the surface tension.
Emulsifying Action of Bile Salts
Bile salts are surface active. They facilitate the action of pancreatic lipase and, hence, absorption of free fatty acids. Bile salts lowers surface tension of fat droplets.
Hay's Test
This test is based on the surface tension and is employed for detecting the presence of bile salts in urine. If urine contains bile salts, the fine sulfur powder sprinkled on its surface settles down due to lowering of surface tension. Fine sulfur powder continues to float on the surface if urine does not contain bile salts.
Role of Surfactant in Lungs
Surfactant is a lipoprotein mixture secreted by special surfactant-secreting cells, i.e., type II granular pneumocytes present in alveolar epithelium (Fig. 1.5). Its surface tension related functions are given below.
Fig. 1.5: Alveolar capillary membrane comprising endothelium, interstitium, epithelium and surfactant lining of part of an alveolus at the junction between two capillaries C1 and C2.
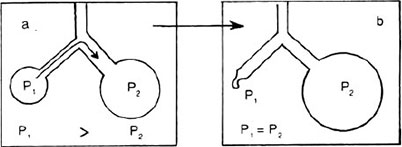
On the basis of Laplace law, air would be displaced from the smaller alveolus into the larger one and the smaller alveolus would thus become still smaller and this process would continue until the smaller alveolus would collapse entirely while displacing all of its air into the larger one. This process would lead to instability of alveoli (Fig. 1.6). But this instability is prevented by surfactant. As an alveolus become smaller the surfactant become more concentrated at the surface of alveolar lining fluid. Hence, surface tension becomes progressively more less. On the other hand as an alveolus becomes bigger, the surfactant is spread more thinly on the fluid surface. This increases the surface tension. This property of surfactant stabilises the sizes of the alveoli, causing the large alveoli to contract more and smaller ones to contract less. The absence of surfactant in the alveolar membrane of some premature infants causes the respiratory stress syndrome in them. Factors reducing production of surfactant or increasing its rate of destruction may contribute to adult respiratory distress syndrome.
Fig. 1.6: Instability of smaller alveolus. If the surface tension in both alveoli were the same (a), the transpulmonary pressure of the smaller alveolus (P1) would exceed that of that larger alveolus (P2). The smaller alveolus would collapse (b) and empty into the larger alveolus
Prevents Alveolar Exudation
The inward force generated by alveolar surface tension increases diffusion of fluids into alveoli from alveolar capillaries. Surfactant, by lowering the pleural pressure decreases the hydrostatic pressure gradient and, therefore, reduces the amount of fluid ultrafiltered. In the absence of surfactant, the surface tension tending to pull fluid into the alveoli increases, causing massive filtration of fluid out of the alveolar wall capillaries into the alveoli, thus filling the alveoli with fluid resulting in oedema.
A sigh is a reflexly generated single deep breath which occurs after a period of quite breathing. Breathing is periodically interrupted by the large inflation of a sigh. This serves to replenish one of the surfactant molecules and restore lung compliance to normal.
Reduces the Work of Breathing
Adsorption of surface-active molecules at the alveolar-air interface reduces the alveolar tension, increasing compliance of the lungs and, thereby, decreasing work of respiration.
Surface-Active Disinfectants
Surface forces which exist between two immiscible liquids and at interface between solid and a liquid are referred to as interfacial tension. Substances that alter the energy relationship at interfaces, producing a reduction of surfaces or interfacial tension, are referred to as surface-active agents. These agents possess both water-attracting (hydrophilic) and water-repelling (hydrophobic groups). Disinfection is achieved by surface tension lowering action of detergents.
Efficient Absorption
Surface tension leads to efficient adsorption. This is applied in:
- enzymatic reactions;
- formation of complex compounds of proteins and lipids, of proteins and salts in cytoplasm; and
- in the action of drugs and poisons.
Surface Tension Model of Muscle Contraction
It is known that actin and myosin filaments of muscle fibres are aligned in a regular pattern with spaces between them so that they can slide past one another. Muscle contraction is produced by sliding of filaments to produce motion. Gamow and Y'cas suggested that this force may be due to surface tension which is present not only in liquids but also in jelly like materials such as muscle cells. Movement of muscle is due to the attraction between the surfaces of two types of filaments. The proposed mechanism, however, was not taken too seriously as actual process of muscle contraction is more complex.
The plasma surface tension is slightly less than water, i.e., surface tension of plasma is 70 dynes/cm while that of water 72.8 dynes/ cm.
Capillary Action and Its Clinical Applications
Capillarity action is employed in estimation of blood clotting time. In this method blood from pricked finger is filled in a fine glass tube capillary by capillary action. Absorbent cotton or gauze used in surgical dressing also work on the principle of capillarity. In addition, capillarity action is employed for a surgical drain.
VISCOSITY
Definition
It is the internal resistance against the free flow of a liquid to the frictional forces between the fluid layers moving over each other at different velocities. According to Newton's law, viscous force F, acting tangentially on a liquid layer is directly proportional to the surface area A of the layer and velocity gradient (dv/dx) in a direction perpendicular to the layer. Velocity gradient is the rate of change of velocity with distance. Hence, the Newton's law can be expressed as:
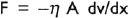
The negative sign indicates that F acts in a direction opposite to the one in which the layer moves, η is a constant of proportionality and is called coefficient of viscosity. It is defined as the tangential force per unit area which resists the flow of two parallel liquid layers past one another when their differential velocity is 1 cm/ sec per centimetre separation. Maxwell considered viscosity of a liquid in motion as closely analogous to ‘rigidity of a solid breaking down continually under a shearing stress’. Hence, viscosity can also be defined as the ratio of shear stress (a tangential force per unit area, F/A, resisting or pushing flow) to shear rate ΔV/ΔX (the change of velocity ΔV between two neighbouring fluid layers divided by their distance, ΔX. Thus:
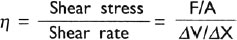
The units of viscosity is ‘Poise’, (P), named in the honour of Poiseuille, the French physicist and physician, who first devised methods for measuring viscosity. Poise is force in dynes, necessary to be applied to an area of 1 cm2 between two parallel planes 1 cm2 in area, and 1 cm apart, to produce a difference in streaming velocity between the liquid planes of 1 cm/sec. Hence, Poise is equal to dyne sec/cm2. Smaller unit is centipoise. Viscosity is also measured in Stoke (ST).
Centipoise (CP) = 0.0I P
Centistoke (CST) = 0.0I ST
Classification of Fluids Showing Viscous Properties
Newtonian Fluids
An ideal or newtonian fluid is one in which the viscosity is constant and is independent of how rapidly the fluid is sheared. Newtonian fluids follow Poiseuille's equation. Plasma is a newtonian fluid even at very high protein concentration.
Non-newtonian Fluids
Non-newtonian fluids change viscosity at different flow velocities. They do not obey Poiseuille's equation. Blood is a non-newtonian fluid because at higher flow rates erythrocytes have tendency to accumulate in the axial laminae. At very slow rates of shear, the suspended cells tend to aggregate.
Viscoelastic Fluids
The fluids which have elastic as well as viscous properties are called viscoelastic fluids. They have a memory for the initial state, i.e. viscoelastic fluids return to its original position after a deformation has ceased. Their deformation is partly dissipative and partly energy storing and rheologically relevant. They are of two types.
Artificial Viscoelastic flow behaviour is found in aqueous solutions of long-chain polymers, gels, colloids and suspensions. Their visco-elasticity can be due to shear induced changes in polymer conformation, changes in structure by aggregation or disaggregation or to the deformation of suspended elastic particles.
18Natural Blood shows natural viscoelasticity. It results primarily from the reversible network building, aggregation and disaggregation of red blood cells. Elastic deformation of red blood cells also contribute to the viscoelasticity.
Types of Viscosities
Relative Viscosity
It is defined as the viscosity of a fluid compared with some other useful standard fluid under the same conditions. In the case of liquids, the reference fluid is usually water.
Kinematic Viscosity
It is the name given to the quantity which is derived by dividing the viscosity by the density. Kinematic viscosity has been related with turbulence. The larger the kinematic viscosity, the less the likelihood of turbulence. The kinematic viscosity increases with haema-tocrit and this decreases the occurrence of turbulence. It is measured in stokes.
Apparent Viscosity
The viscosity calculated from Poiseuille's law at any particular flow and tube diametre; it is used for suspensions, such as blood that exhibits Fahraeus-Lindqvist effect and anomalous viscosity.
Anomalous Viscosity
The viscous behaviour of non-homogeneous fluids or suspensions, such as blood, in which the apparent viscosity increases as flow or shear rate decreases toward zero.
Intrinsic Viscosity
It is used for biopolymers like proteins. Proteins in their native state exist as rather compact structures. This can be appreciated directly from a consideration of the hydrodynamic behaviours of proteins. Intrinsic viscosity is defined as:

19where V is the volume of the particle, m is its mass, and A is a function of the axial ratio of the molecule and is equal to 2.5 for rigid spheres and increases with increasing axial ratio. Intrinsic viscosity (η) of biopolymers is related to its hydrodynamic volume Vh by equation:
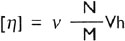
where ‘ν’ is called increment or Simha's factor, M is molecular weight of the biopolymer and N is Avogadro's number. The hydrodynamic volume of the biopolymer is its volume plus the volume of the solvent imbibed within the biopolymer molecule. The value of ‘ν’ for globular proteins lie between 3 and 10. For asymmetric proteins such as collagen, ‘ν’ is 1200 and is about 7000 for some samples of DNA. The viscosity increment depends on the degree of hydration of biopolymer and its asymmetry. Hence, marked increase in [η] occurs on unfolding the polypeptide chain by cleavage of disulfide bridges or by treatment with concentrated solution of urea.
Limiting Viscosity Number
Solutions of native DNA have a very high viscosity. By finding the limiting viscosity number one can characterise the biopolymer in term of its size, shape and conformation. The limiting viscosity number can be defined in terms of [η] by the equation:
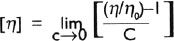
where C is the concentration of biopolymer in grams per milimetre, η is the viscosity of the solution, and η0 is the viscosity of the pure solvent. The fraction η/η0 is relative viscosity, and the quantity [(η/η0)−1] is referred to as the specific viscosity. When the concentration C is expressed in grams per decilitre, the parameter defined by above equation is usually called intrinsic viscosity which is, therefore, given in units of decilitre per gram.
Factors Affecting Viscosity
Density
Viscosity is directly proportional to density. If a small sphere of radius ‘r’ and density ‘p’ falls vertically through a liquid of density20 ‘p’ at a steady velocity ‘u’ in spite of the acceleration due to gravity ‘g’, then the coefficient of viscosity of the liquid is given by the equation:

This is called Stoke's law.
Temperature
With the increase in temperature, viscosity of solution falls. This is due to increase in kinetic energy of molecules for overcoming the resistance due to intermolecular attractions and also for breaking intermolecular H bonds of associated liquid.
Shape and Size of Solute Particles
Viscosity varies directly with the size and asymmetry of solutes or suspended particles. Hence, a solution of deoxyribonucleoprotein is more viscous than that of fibrinogen. Because it has the tertiary structure of fibrous type while fibrinogen has a long rod-like shape. All the fibrous protein solutions are more viscous than those of globular proteins. Highly asymmetrical molecules show a high intrinsic viscosity compared with spherical molecules of same molecular weight.
Molecular weight Other factors being comparable, the viscosity is a function of the molecular weight and this relationship is given by (η) = KMa’, where M is the molecular weight, (η) is intrinsic viscosity, and K and ‘a’ are constants.
Electrolytes
The electrolytes exert deleterious effect on the viscosity of a solution.
Hydrogen Bonds
Disruption of hydrogen bonds produce a marked decrease in the viscosity.
Colloidal State
Viscometers
Different viscometers employed for viscosity determination are described below.
Denning and Watson's Viscometer
It is a simple apparatus consisting of U-shaped capillary tube. One arm of this U is long while the other is much shorter. The end of the long arm is expanded into funnel so that blood can easily be collected into it. The short arm contained a bulb. On either side of bulb there is a mark. The lower side of the bulb has a mark 1 and upper side a mark 2, as shown in Figure 1.7A.
Hess Viscometer
It consists of two capillaries of equal bore and equal length, connected by T tube with suction bulbs. Simultaneously, blood is sucked through one capillary and water through the other. The relative viscosity of blood as compared with that of water is determined from the volumes of water and blood that have flowed through the capillaries, the viscosities being inversely proportional to the volume of flow for a given time.
Ubbelohde Viscometer
Structure of this viscometer is shown in Figure 1.7B. It has a pair of scratches at B and C. The upper scratch is for timing the movement of meniscus from A to B and lower from B to C. The double scratch is to allow time to restart a stopwatch. The relative shear gradients 22are usually calculated from constants provided by manufacturer. In this viscometer shear gradient cannot be varied and solutions must be relatively fine to avoid clogging the fine capillary. The solution is added from opening I. The liquid falls owing to the difference in height between the two arms, i.e., the hydrostatic head. The time ‘t’ required for meniscus to move between A and B is measured.
Couette Viscometer
It consists of two concentric cylinders separated by a narrow annulus, which is filled with the sample. One cylinder is fixed and the other rotates. In this viscometer, the shear gradient is fixed and shear stress is measured.
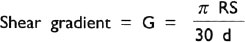
where R is the average radius of the cylinder, S is the rotor speed in rpm, and ‘d’ is the annular distance.
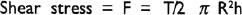
where ‘h’ is the height of the cylinder and T is the torque necessary to maintain the speed ‘S’.
Rolling Ball Viscometers
Here, a metal sphere is allowed to fall under the influence of gravity through a viscous fluid, it accelerates at first but then achieves a constant velocity-called the terminal velocity. At terminal velocity, the downward net force on the ball is balanced by the opposing force produced by the viscous resistance of the fluid. For a given ball-bearing falling through a viscous fluid for a known distance, the terminal velocity is proportional to the difference in densities between the sphere and the fluid and is inversely proportional to the viscosity of the fluid.
Ostwald Viscometer
It is a U-shaped tube whose limbs has the same length (Fig. 1.7C). It has got two bulbs, one ending into wider vertical tube, i.e., on right hand side and other ending into a capillary tube, i.e., on the left hand side of the figure. The right hand bulb is filled with the test liquid via the wide vertical tube. The test fluid is then sucked up into the narrow limb to above point 1. The time taken to fall 23from 1 to 2 is measured both for the test liquid and for water. The relative viscosity measured through Ostwald viscometer is expressed as:
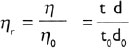
where ‘η’ and ‘η0’ are viscosities of test solution and water having density ‘d’ and ‘d0’. Time taken by solution and water to flow are noted as ‘t’ and ‘t0’.
Biomedical Importance of Viscosity
Viscosity of Blood
Blood is a suspension of cells in plasma. Plasma is a water solution of salts and heavily hydrated macromolecules. Blood cells behave as suspended particles and increase the viscosity of blood. Fibrinogen due to its anisometric character, high density, and nearly neutral charge imparts maximum viscosity to the blood. Globulins have greater influence than albumin. Plasma has a normal viscosity of 15 to 20 mpoises at 20°C. Viscosity of the whole blood ranges from 30 to 40 mpoises at 20°C.
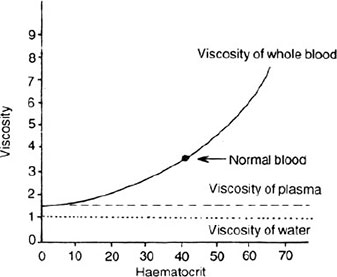
Effect of erythrocytes on the viscosity of blood Due to deform-ability, erythrocytes when freely suspended assume biconcave discoid shape, indicative of the large excess of its surface area over its volume. Deformability is reduced by low pH and low oxygen tension. Deformability affects viscosity of blood in small vessels. In sickle-cell anaemia, the desaturated haemoglobin is crystallined and it reduces the deformability of erythrocytes, thereby, affecting the viscosity of blood. Viscosity of blood also varies with changing haematocrit. When the haematocrit rises, the friction between the successive layers of the blood increases. Hence, with increasing haematocrit the viscosity of the blood rises drastically (Fig. 1.8), e.g. when haematocrit rises to 60 to 70%, the viscosity of blood becomes as great as 10 times that of water. Increased viscosity increases the peripheral resistance, thereby, the blood pressure leading to hypertension. Increased viscosity tends to decrease the rate of venous return to the heart. In severe anaemia, the viscosity of blood is reduced to half. This decreases the resistance to blood flow in the peripheral vessels, Hence, greater quantities of blood return to the heart. This leads to increased cardiac output and hence, increased work load on the heart. In vivo, the effective viscosity of blood 24passing through capillaries is 50% that of in large vessels.
This is because the erythrocytes in capillaries travel through a single file. It is also known as plug flow. The fact that blood flow in very minute vessels exhibit far less viscous effect is called Fahraeus-Lindqvist effect.
Effect of temperature on the viscosity of blood This is due to the presence of thermoproteins, which show physical changes at temperature below or above 37°C. Cryglobulin operate at temperature below 37°C forming reversible or irreversible precipitates, gels or crystals. Pyroglobulin gets precipitated at 56°C. Bence-Jones proteins get precipitated at 40°C, At 0°C, the viscosity of blood is increased up to three times. This reduces the circulation in the tissues exposed to cold.
Effect of inflammation on the viscosity of blood Inflammation causes loss of plasma into the tissues. This leads to slowing of blood flow, disturbance in the axial flow, rouleaux formation and increase in viscosity (Fig. 1.9).
Effect of diseased conditions on the viscosity of blood Viscosity of blood is increased in diabetes mellitus, multiple myeloma, jaundice, leukaemia, asphyxia, vomiting and diarrhoea.
Viscosity of Synovial Fluid
Synovial fluid is highly viscous. Its viscosity varies from 50 to 200 times that of water. The high viscosity of synovial fluid is due to 25the presence of hyaluronic acid (0.85 g/dl).
The viscosity of synovial fluid is determined by falling drop method. For this, joint fluid is aspirated into a pipette and then released. If the falling drop of joint fluid is drawn out into a 5 cm long or longer tenacious band, the viscosity is normal. If the drop falls like water then viscosity is low. Viscosity of synovial fluid reflects its hyaluronic acid content. In inflammatory effusions as seen in rheumatoid arthritis, septic arthritis and gout the viscosity of synovial fluid is markedly decreased, indicating the presence of a thin watery fluid containing degraded small molecular hyaluronidase particles.
Viscosity of Gels
Dietary fibre is a complex carbohydrate. Non-starch polysaccharides that are soluble in water form viscous solutions or gels. Viscous properties of this gel delays gastric emptying, reduce absorption from small intestine, cause greater exposure of ileum to fat. The presence of fat in the ileum suppresses the motility of stomach and proximal small intestine and, hence, induces satiety sensation earlier to a meal(s).